Estadística Inferencial: de la muestra a la población

Bienvenidos a esta nueva edición de Mundo Tarea Virtual sobre la Estadística Inferencial. En la mayoría de los casos, cuando se analizan datos numéricos en contextos investigativos se hace necesario trabajar con estadística, para obtener resultados fehacientes. La estadística inferencial tiene que ver estadígrafos, los cuales surgen del análisis de variables objeto de estudio, tratados de formas numéricas y son considerados como los resultados de la investigación.

Para la obtención de los resultados, se hace necesario en la mayoría de los casos trabajar con software o paquetes estadísticos creados especialmente para ello. Desde el momento en que se tiene la información numérica (resultados) pueden hacerse inferencias o conclusiones, de allí el nombre Estadística Inferencial. Un aspecto que se ha de resaltar es que estas inferencias son aplicadas a la muestra seleccionada y puede extrapolarse a la población investigada.

Ahora bien hay que dejar claro que la estadística está dirigida a investigaciones cuantitativas y es prácticamente nulo en investigaciones con enfoque cualitativo. El análisis numérico se estructura para estudios con escalas, preguntas cerradas, análisis de frecuencias, variables implicadas, entre otros aspectos. Un análisis documental de corte histórico, psicológico, estudio de casos que tengan datos bibliográficos, poco tendrá que ver con la estadística inferencial.

1. ¿Para qué es útil la Estadística Inferencial

La estadística es una rama de la matemática que apoya eficientemente el desarrollo de investigaciones, ayuda a establecer comparaciones o correlaciones, impulsa el análisis numérico y la extrapolación de los resultados desde la muestra a la población seleccionada. Por tanto, es muy útil para analizar variables y obtener resultados con una mayor validez y confiabilidad.

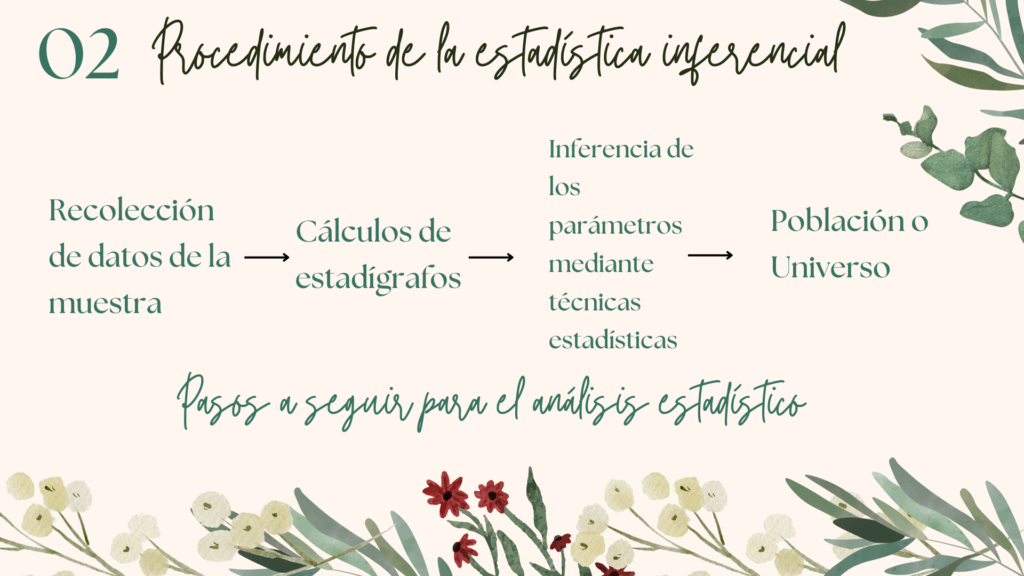
2. Procedimiento de la Estadística Inferencial

Ahora bien, ¿Cuál es el procedimiento adecuado que ha de seguirse para realizar el análisis estadístico?

Inicialmente, con ayuda de técnicas e instrumentos cuidadosamente seleccionados se procede a la recolección de datos en la muestra seleccionada.

Luego, los datos son trabajados en paquetes estadísticos y se calculan los estadígrafos.

A continuación, con los resultados obtenidos se procede a la inferencia de los parámetros mediante técnicas estadísticas.

Y finalmente, se procede a analizar la información en el contexto de la población o universo seleccionado

3. Uso de la Estadística Inferencial à Prueba de hipótesis

Entre los elementos que destacan al realizar una investigación cuantitativa es que el análisis matemático está direccionado a evaluar las hipótesis propuestas y llegar a conclusiones generales sobre ello. La información ayuda a realizar adecuadamente los análisis de resultados. Sin embargo, es importante reconocer que en esta prueba de hipótesis es importante reconocer que:

Es una proposición respecto a uno o varios parámetros que son analizados.

Si la hipótesis es consistente con los datos, ésta es retenida como un valor aceptable del parámetro.

Si la hipótesis no es consistente con los datos, se rechaza ésta (pero los datos no son descartados (Wiersma, 1986).

4. ¿Qué es una distribución muestral en el contexto de la estadística inferencial?

Un aspecto importante a considerar al realizar los análisis estadísticos inferenciales, es la distribución muestral considerada por Wiersma (1986) como: “un conjunto de valores sobre una estadística calculada de todas las muestras posibles de un determinado tamaño” (p.337).

Por tanto, para calcular la distribución muestral se requiere valorar las medias de todas las muestras del mismo tamaño (n) que se han obtenido de la misma población. Es importante recordar que la muestra se estructura como una parte de la población que ha de ser representativa para poder extrapolar los resultados a todo el conjunto de sujetos que conforma esta población.

5. Características de una Distribución Muestral en el marco de la Estadística Inferencial

Existen algunos aspectos importantes a resaltar dentro del significado de una distribución muestral, entre los que destacan:

Es unimodal, una sola moda, lo cual significa que, en ese modo único, la frecuencia máxima es significativamente mayor que las otras.

La asimetría es cero, mostrando que la mitad de la curva es exactamente igual a la otra mitad.

Refiere una función particular entre desviaciones con respecto a la media de una distribución y la probabilidad de que éstas ocurran.

Es mesocúrtica lo cual refiere una curtosis de cero. Esto significa que suele mostrar un grado de concentración medio alrededor de los valores centrales de la variable objeto de investigación. Finalmente, en la distribución muestral: la media, mediana y moda coinciden en el mismo punto.

6. ¿Qué es el nivel de significancia? ¿Por qué es importante para la estadística inferencial?

Uno de los elementos importantes que se deben tomar en cuenta para el análisis de resultados y discriminar adecuadamente las observaciones realizadas es el nivel de significancia. En este aspecto se puede señalar que:

El nivel de significancia es un valor de certeza que fija el investigador “a priori”.

El propósito del investigador al efectuar el análisis estadístico es conocer si la probabilidad de la media de la muestra está cerca de la media de la distribución muestral (si es grande o pequeña).

En el caso de que la distancia a la media (distribución muestral) sea pequeña, el investigador dudará de generalizar a la población. Si es grande, el investigador podrá hacer generalizaciones. El nivel de significancia o nivel alfa (nivel a) refiere el valor al equivocarse y genera la oportunidad de obtener la confianza necesaria en la investigación. Por lo tanto, muestra un posible acercamiento a la distribución muestral.

7. ¿Cómo trabajar con el nivel de significancia en el contexto de la estadística inferencial?

Una vez profundizado en la concepción del nivel de significancia surge la duda de cómo el investigador debe trabajarlo. Para ello, es necesario tomar en cuenta algunos aspectos:

1. Realizar el análisis estadístico y obtener la media en la muestra seleccionada.
2. Analizar el porcentaje de confianza, revisando si éste se acerca o distancia de la distribución muestral.
3. Verificar cuál es el valor del porcentaje más alta y optar por ello para alcanzar mayor probabilidad de éxito.
4. Evitar un error de muestreo al trabajar con un nivel de significancia que le permita generalizar a toda la población.

8. ¿Qué porcentaje de confianza requiere un investigado para generalizar? ¿Cómo se traduce esto al nivel de significancia?

Resulta que en la medida en que el porcentaje se acerque el a100% se alcanza una mayor confianza. Esto quiere decir que se pueden considerar con mayor fuerza que los resultados son veraces y por lo tanto bien tratados estadísticamente. En tal sentido, existen dos niveles de significancia recomendados:

1. El nivel de significancia del 0,05 el cual refiere que existe un 95% de seguridad de que el investigador generalice sus resultados sin inconveniente alguno. Para entender un poco esto, es posible señalar que en términos de probabilidad tomar en cuenta el 0,95 y 0,05 respectivamente al sumarlos dan la unidad (valor muy usado a nivel estadístico en donde en un evento “X” cero nunca ocurrirá y uno seguro que si ocurrirá). De manera que obtener un 0,05 nivel de significancia indicará que existe un 95% de probabilidad que ocurra un evento, que sea veraz una correlación (en el caso de que esto se esté estudiando), que haya significatividad de los resultados obtenidos, entre otros aspectos.
2. El nivel de significancia del 0,01 lo cual implica que el investigador tiene un 99% a favor para generalizar sin temor y un 1% en contra (al sumar 0,99 y 0,01 se obtiene el 1). Por tanto, las investigaciones que alcanzan este nivel de significancia tienen gran oportunidad de generalizar a toda la población los resultados obtenidos. Siempre es mejor alcanzar un 99% de confianza que un 95%; sin embargo, al ser mayor a 90% se habla de una buena significatividad.

¿Cómo se relacionan la distribución muestral y el nivel de significancia?

Entre los aspectos que relacionan la distribución muestral y el nivel de significancia se destaca que ambos tienen que ver directamente con un término llamado probabilidad. En el nivel de significancia se expresa en términos de probabilidad (0,05 y 0,01) y la distribución muestral también tiene que ver con probabilidad (el área total de ésta como 1,00).

En efecto, el investigador necesita valorar si existe confianza o no al generalizar los resultados alcanzados. Por tanto, al generalizar cada investigador se apoya en la distribución muestral la cual es considerada como una probabilidad apropiada para la investigación social. Por su parte, el nivel de significancia representa las posibles áreas de riesgo o confianza en la distribución muestral.